EDA数据探索性分析
EDA目标
- EDA的价值主要在于熟悉数据集,了解数据集,对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用。
- 当了解了数据集之后我们下一步就是要去了解变量间的相互关系以及变量与预测值之间的存在关系。
-
引导数据科学从业者进行数据处理以及特征工程的步骤,使数据集的结构和特征集让接下来的预测问题更加可靠。
on run {input, parameters} set filename to POSIX path of input set cmd to "clear; cd `dirname " & filename & "`;vim " & quote & filename & quote tell application "iTerm" activate tell the current window create tab with default profile tell the current session write text cmd end tell end tell end tell end run
step1:载入各种数据科学以及可视化库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
Train_data:150000 rows × 31 columns
Test_data:50000 rows × 30 columns
-
简略观察数据:
Train_data.head().append(Train_data.tail()) -
通过
.describe()来熟悉数据的相关统计量describe种有每列的统计量,个数count、平均值mean、方差std、最小值min、中位数25% 50% 75% 、以及最大值。看这个信息主要是瞬间掌握数据的大概的范围以及每个值的异常值的判断,比如有的时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式,有的时候需要注意下
Field Description 数据情况 SaleID 交易ID,唯一编码 唯一编码 name 汽车交易名称,已脱敏 【无有效信息】 regDate 汽车注册日期,例如20160101,2016年01月01日 最早注册日期19910001、最晚20151212 model 车型编码,已脱敏 [0-247] 种车型【有缺失值】 brand 汽车品牌,已脱敏 [0-39] 种品牌 bodyType 车身类型:豪华轿车:0,微型车:1,厢型车:2,大巴车:3,敞篷车:4,双门汽车:5,商务车:6,搅拌车:7 [0-7] 种车身类型【有缺失值】 fuelType 燃油类型:汽油:0,柴油:1,液化石油气:2,天然气:3,混合动力:4,其他:5,电动:6 [0-6] 种燃油类型【有缺失值】 gearbox 变速箱:手动:0,自动:1 [0-1] 种变速箱【有缺失值】 power 发动机功率:范围 [ 0, 600 ] max值19312【该字段存在异常值】 kilometer 汽车已行驶公里,单位万km [0-15] 万行驶里程 notRepairedDamage 汽车有尚未修复的损坏:是:0,否:1 [0-1] 是否损坏 regionCode 地区编码,已脱敏 【无有效信息】 seller销售方:个体:0,非个体:1[0-1] 种销售【无有效信息】【数据倾斜】offerType报价类型:提供:0,请求:1最大值为0【无有效信息】【数据倾斜】creatDate 汽车上线时间,即开始售卖时间 最早售卖日期20150618、最晚20160407 price 二手车交易价格(预测目标) 最大值99999,与75%中位数7700差距较大【该字段存在异常值】 v系列特征 匿名特征,包含v0-14在内15个匿名特征 v_2,v_3,v_4,v_10,v_11,v_12,v_13,v_14【最大值与75%中位数和均值差距较大】 -
info 通过info来了解数据每列的type,有助于了解是否存在除了nan以外的特殊符号异常
-
notRepairedDamage 为object类型,其余为float
-
Train_data.isnull().sum()查看每列的存在nan情况
-
# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()
# 通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印,主要的目的在于 nan存在的个数是否真的很大,如果很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉
```bash
# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()
# 通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印,主要的目的在于 nan存在的个数是否真的很大,如果很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉
```
```python
# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()
# 通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印,主要的目的在于 nan存在的个数是否真的很大,如果很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉
```
<p align="center">
<img src="https://github.com/Julian-young/Julian-young.github.io/raw/master/uPic/vVwylt.png" style="zoom:50%" />
</p>
step2: 判断数据缺失和异常
-
可视化查看缺省值:测试集的缺省和训练集的差不多情况, 可视化有四列有缺省,fuelType缺省得最多
msno.matrix(Train_data.sample(250))

msno.bar(Train_data.sample(1000))

-
查看异常值检测:可以看出来‘ - ’也为空缺值,因为很多模型对nan有直接的处理,这里我们先不做处理,先替换成nan
Train_data['notRepairedDamage'].value_counts()0.0 111361 - 24324 1.0 14315 Name: notRepairedDamage, dtype: int64 -
以下两个类别特征严重倾斜,一般不会对预测有什么帮助,故这边先删掉

step3:了解预测值分布
-
总体分布概况(无界约翰逊分布等)
import scipy.stats as st y = Train_data['price'] plt.figure(1); plt.title('Johnson SU') sns.distplot(y, kde=False, fit=st.johnsonsu) plt.figure(2); plt.title('Normal') sns.distplot(y, kde=False, fit=st.norm) plt.figure(3); plt.title('Log Normal') sns.distplot(y, kde=False, fit=st.lognorm)

- 价格不服从正态分布,所以在进行回归之前,它必须进行转换。虽然对数变换做得很好,但最佳拟合是无界约翰逊分布
-
查看skewness and kurtosis
## 2) 查看skewness and kurtosis sns.distplot(Train_data['price']); print("Skewness: %f" % Train_data['price'].skew()) print("Kurtosis: %f" % Train_data['price'].kurt())
- 偏度(Skewness):是描述数据分布形态的统计量,其描述的是某总体取值分布的对称性,简单来说就是数据的不对称程度。当数据变得更加对称时,它的偏度值会更接近零。
- 峰度(Kurtosis):偏度是描述某变量所有取值分布形态陡缓程度的统计量,简单来说就是数据分布顶的尖锐程度。峰度表示分布的尾部与正态分布的区别。
-
查看预测值的具体频数
## 查看预测值的具体频数 plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red') plt.show()
- 处理方法:查看频数, 大于20000得值极少,其实这里也可以把这些当作特殊得值(异常值)直接用填充或者删掉。也可以进行log变换进行预测,这也是预测问题常用的trick。

Step4.1:类别特征查看unique分布
-
数字特征:
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ] -
类别特征:
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]Field Description 数据情况 name 
99662个不同值 model 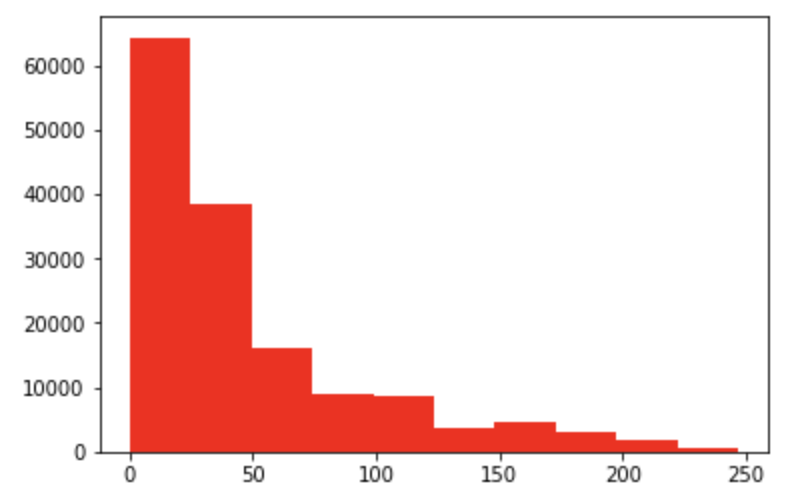
248个不同值 brand 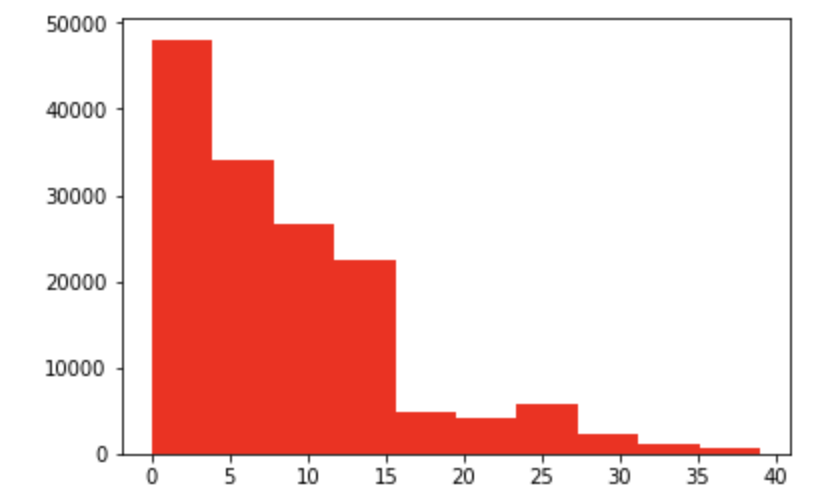
40不同的值 bodyType 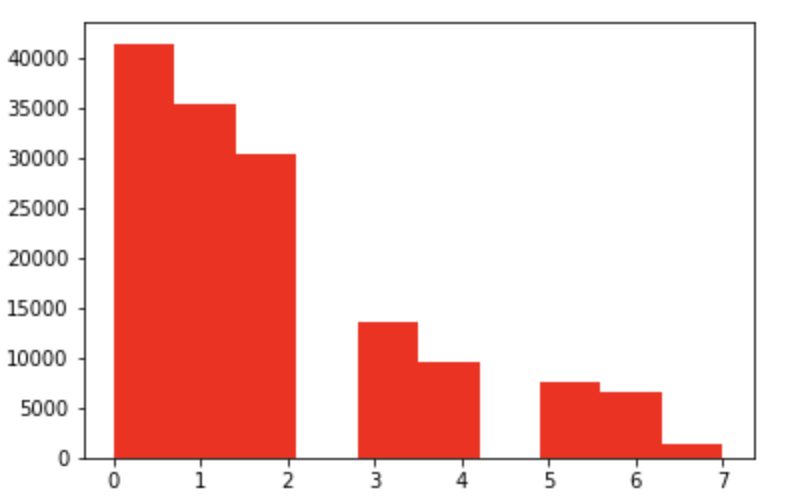
8不同的值 fuelType 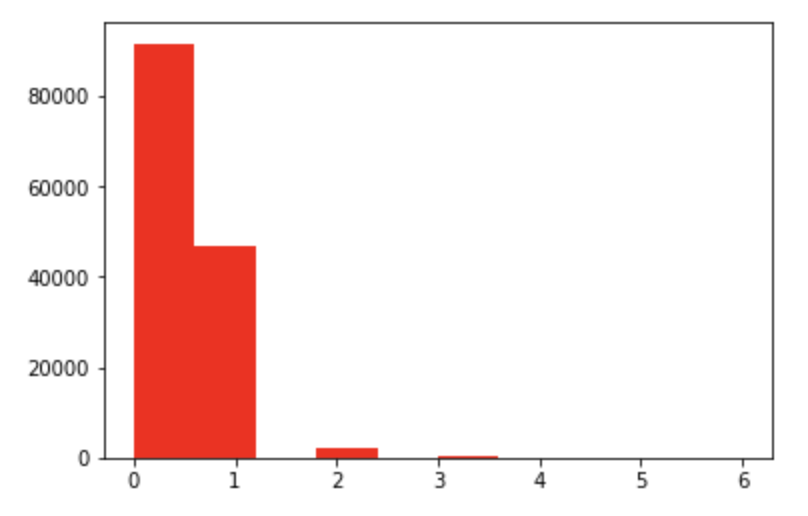
7不同的值 gearbox 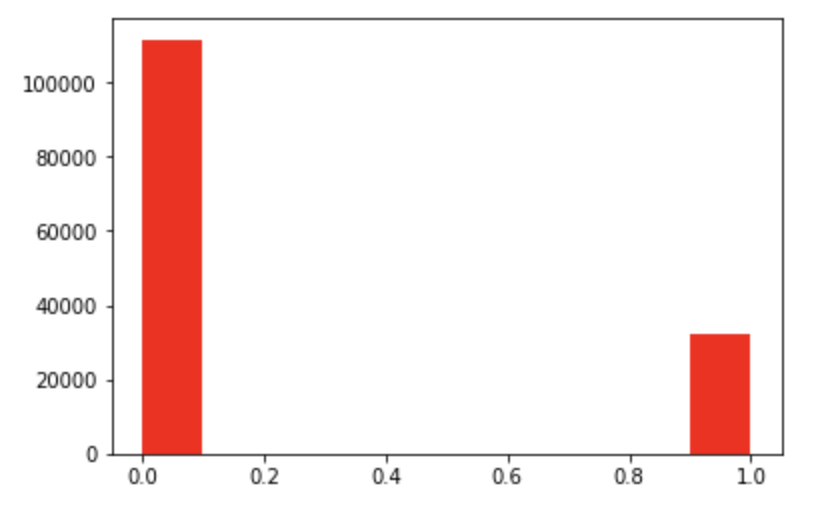
2不同的值 regionCode 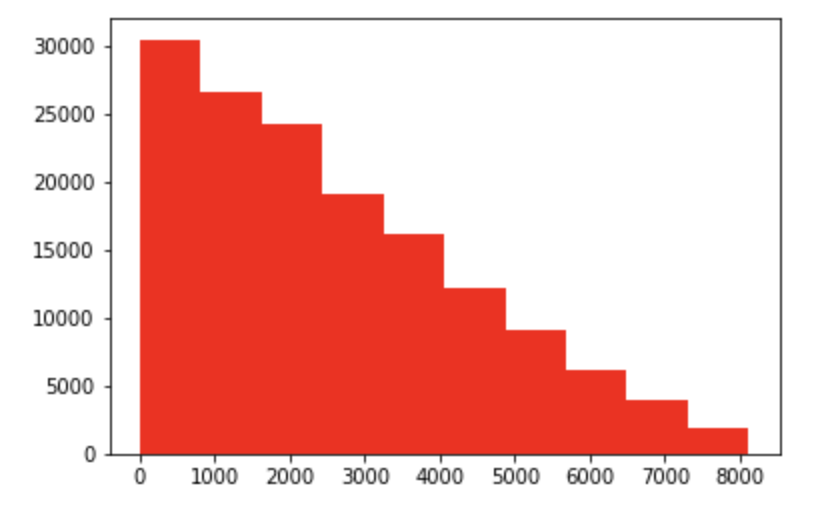
7905不同的值 notRepairedDamage (0.0,111361) (1.0,14315) 2不同的值
step4.2:数字特征分析
-
相关性分析:混淆矩阵
price_numeric = Train_data[numeric_features] correlation = price_numeric.corr() print(correlation['price'].sort_values(ascending = False),'\n') >>> price 1.00 v_12 0.69 v_8 0.69 v_0 0.63 power 0.22 v_5 0.16 v_2 0.09 v_6 0.07 v_1 0.06 v_14 0.04 v_13 -0.01 v_7 -0.05 v_4 -0.15 v_9 -0.21 v_10 -0.25 v_11 -0.28 kilometer -0.44 v_3 -0.73 Name: price, dtype: float64 f , ax = plt.subplots(figsize = (12, 12)) plt.title('Correlation of Numeric Features with Price',y=1,size=16) sns.heatmap(correlation,square = True, vmax=0.8)
-
看几个特征的偏度和峰值
for col in numeric_features: print('{:15}'.format(col), 'Skewness: {:05.2f}'.format(Train_data[col].skew()) , ' ' , 'Kurtosis: {:06.2f}'.format(Train_data[col].kurt()) ) >>> power Skewness: 65.86 Kurtosis: 5733.45 kilometer Skewness: -1.53 Kurtosis: 001.14 v_0 Skewness: -1.32 Kurtosis: 003.99 v_1 Skewness: 00.36 Kurtosis: -01.75 v_2 Skewness: 04.84 Kurtosis: 023.86 v_3 Skewness: 00.11 Kurtosis: -00.42 v_4 Skewness: 00.37 Kurtosis: -00.20 v_5 Skewness: -4.74 Kurtosis: 022.93 v_6 Skewness: 00.37 Kurtosis: -01.74 v_7 Skewness: 05.13 Kurtosis: 025.85 v_8 Skewness: 00.20 Kurtosis: -00.64 v_9 Skewness: 00.42 Kurtosis: -00.32 v_10 Skewness: 00.03 Kurtosis: -00.58 v_11 Skewness: 03.03 Kurtosis: 012.57 v_12 Skewness: 00.37 Kurtosis: 000.27 v_13 Skewness: 00.27 Kurtosis: -00.44 v_14 Skewness: -1.19 Kurtosis: 002.39 -
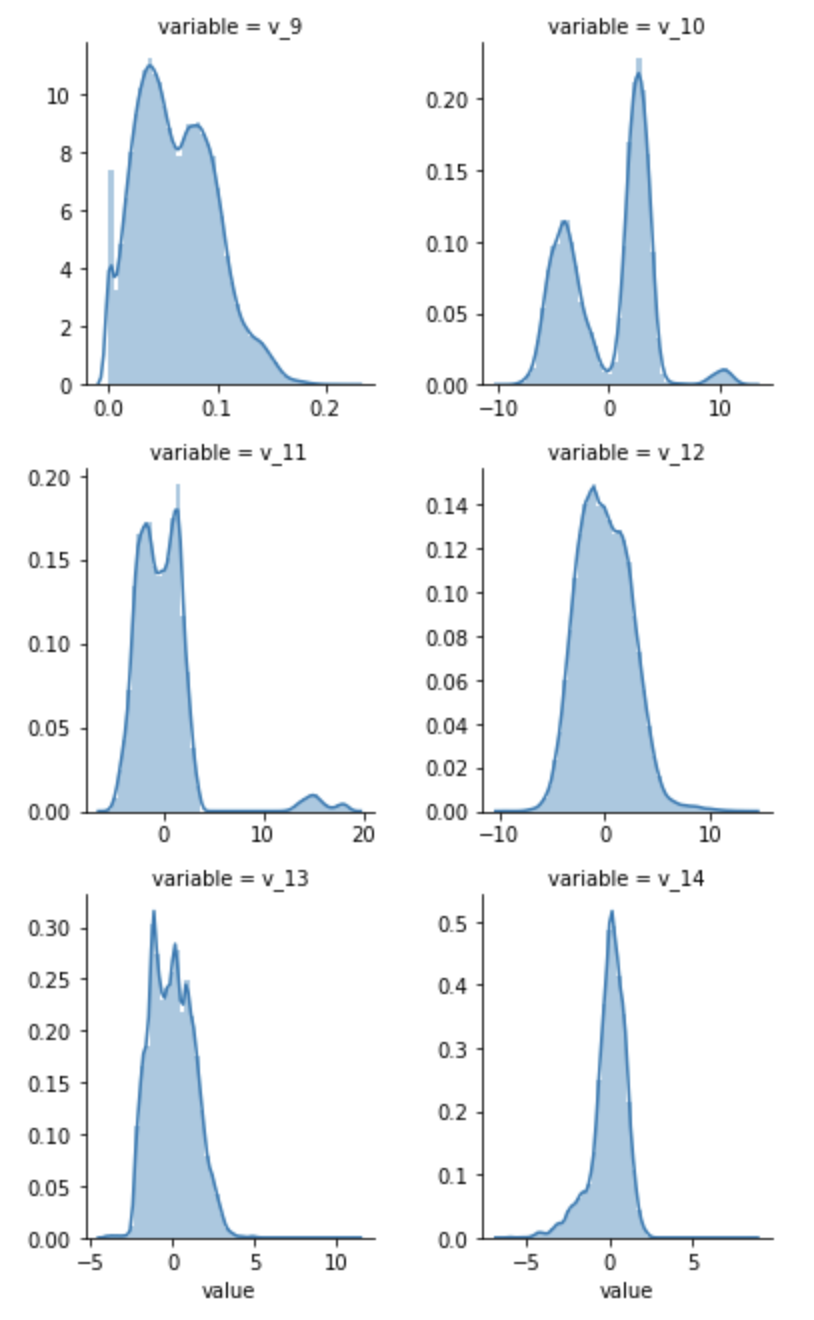
每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features) g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False) g = g.map(sns.distplot, "value")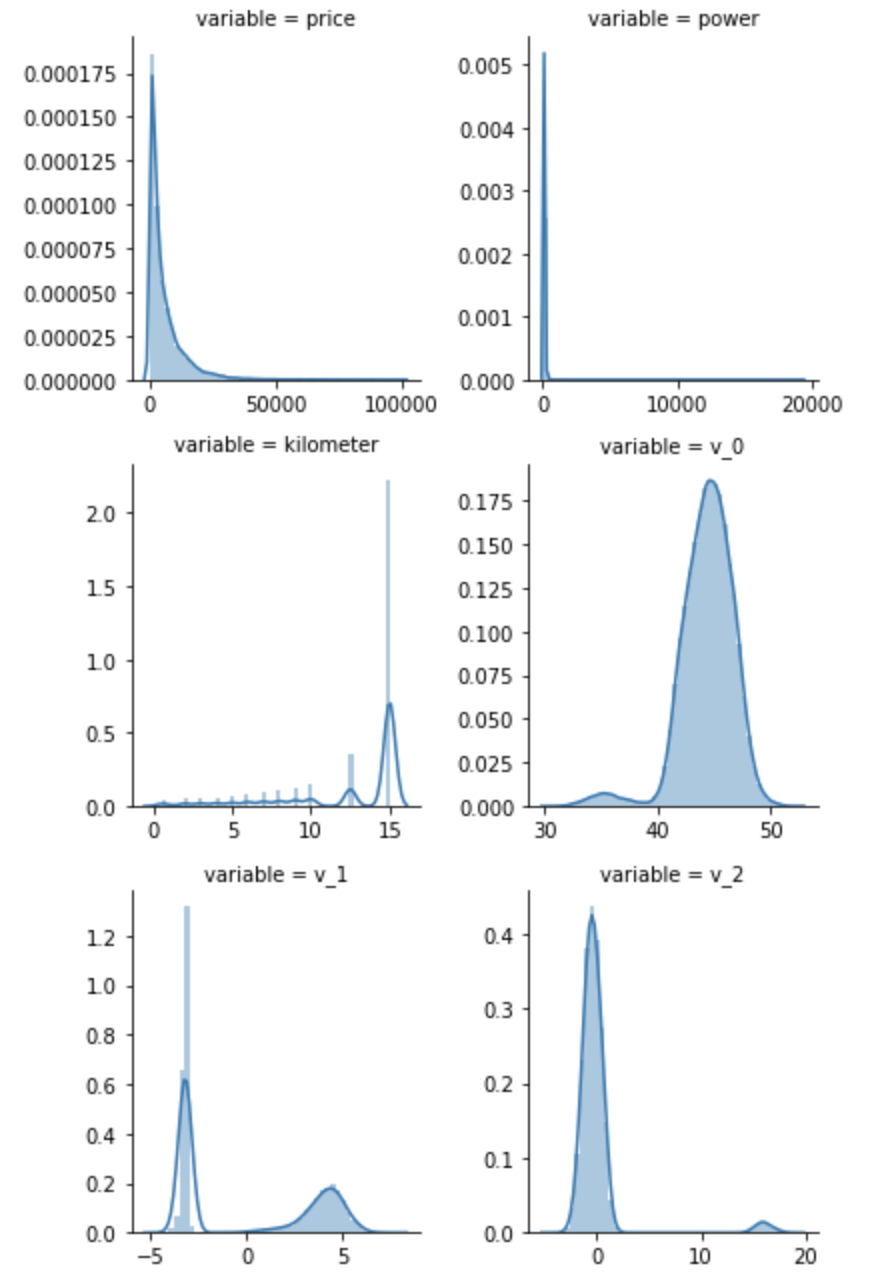
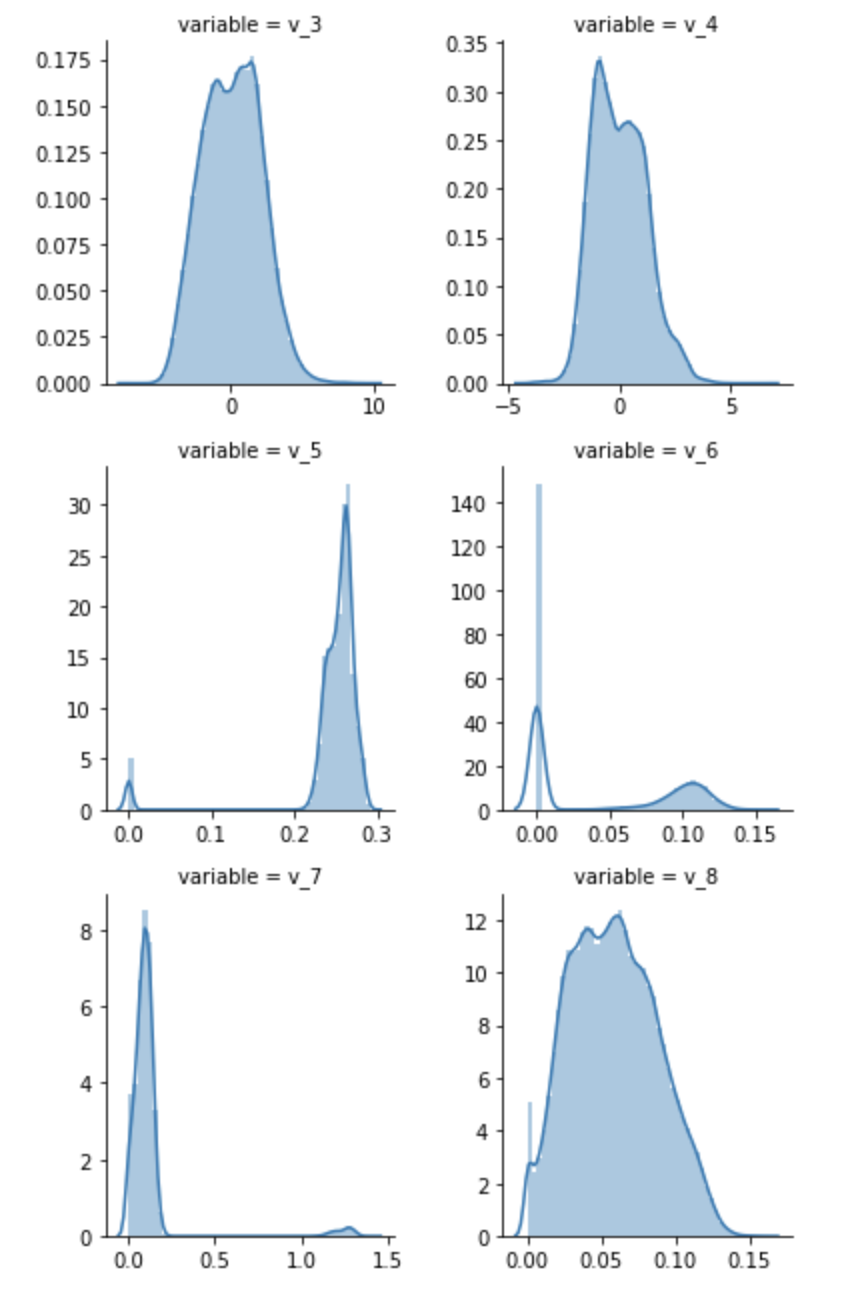
-
数字特征相互之间的关系可视化
sns.set() columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14'] sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde') plt.show()
-
多变量互相回归关系可视化
## 5) 多变量互相回归关系可视化 fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20)) # ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14'] v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1) sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1) v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1) sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2) v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1) sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3) power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1) sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4) v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1) sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5) v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1) sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6) v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1) sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7) v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1) sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8) v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1) sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9) v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1) sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)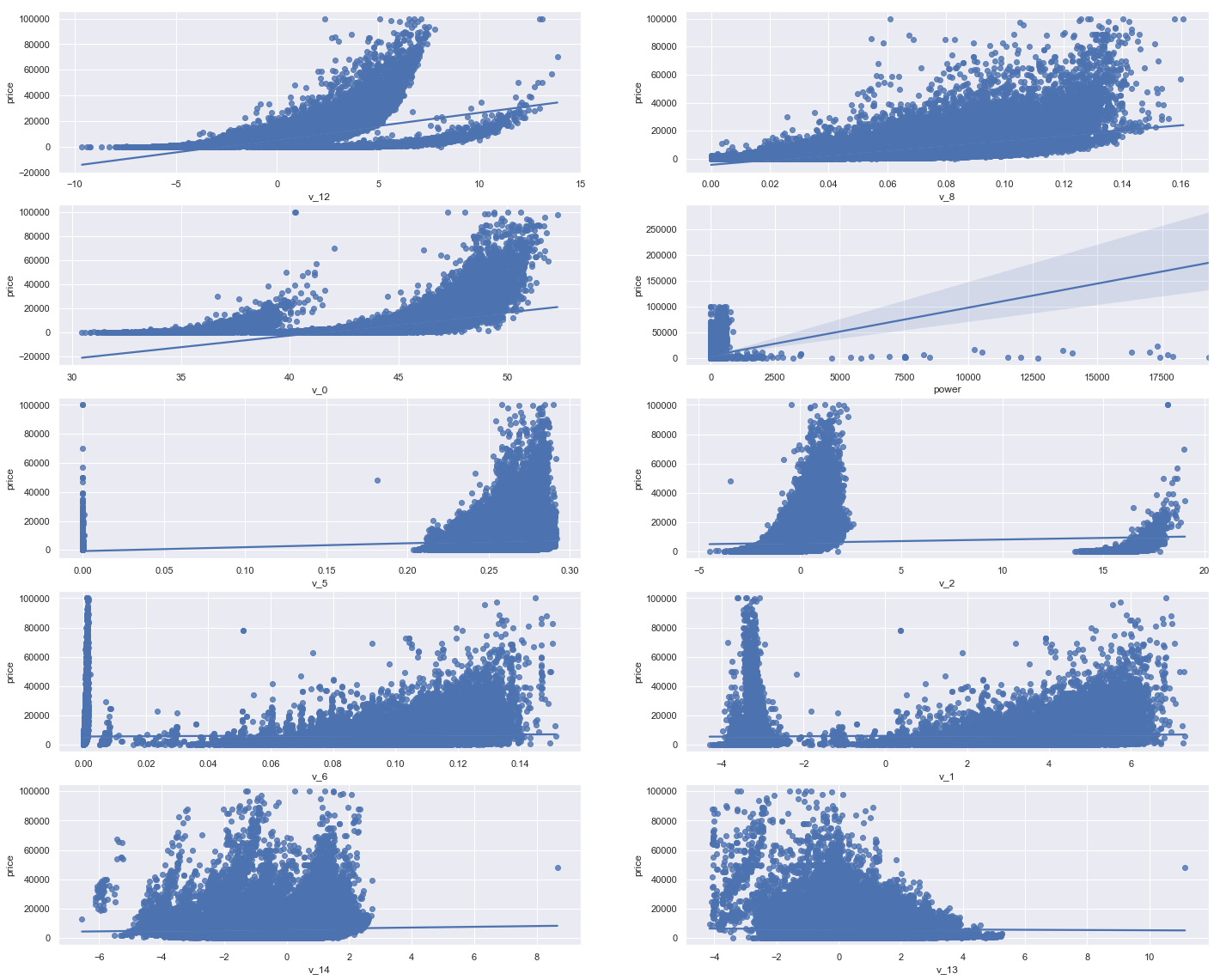
stpe4.3:类别特征分析
-
类别特征箱形图可视化
categorical_features = ['model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage'] for c in categorical_features: Train_data[c] = Train_data[c].astype('category') if Train_data[c].isnull().any(): Train_data[c] = Train_data[c].cat.add_categories(['MISSING']) Train_data[c] = Train_data[c].fillna('MISSING') def boxplot(x, y, **kwargs): sns.boxplot(x=x, y=y) x=plt.xticks(rotation=90) f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features) g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5) g = g.map(boxplot, "value", "price")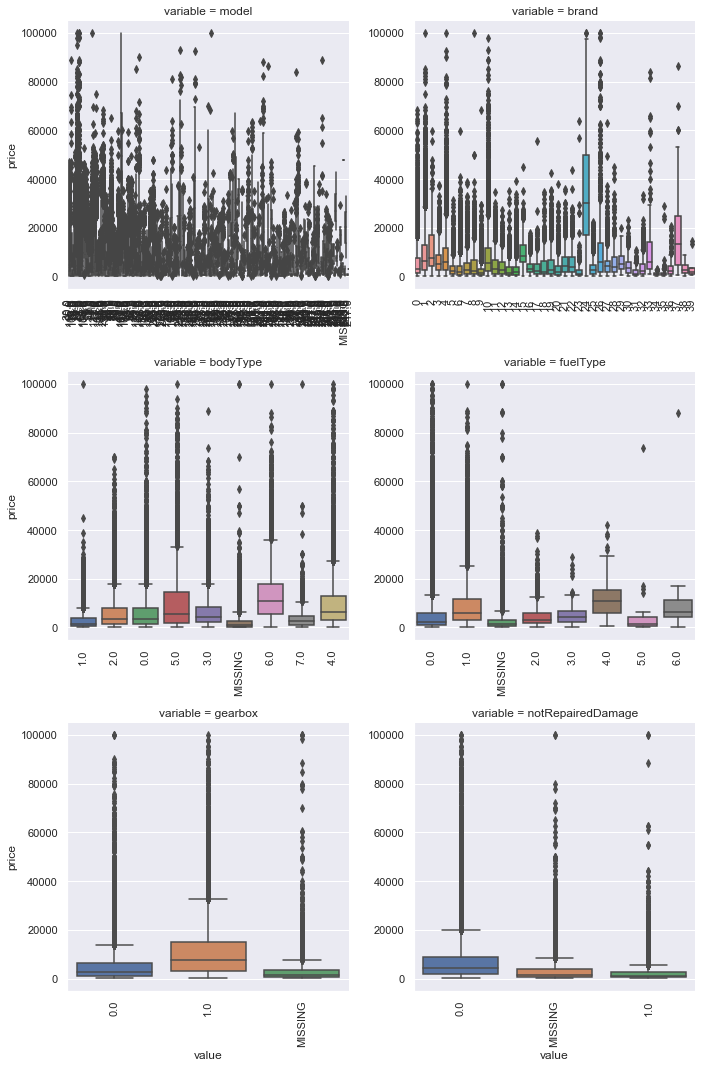
总结
-
可视化分析参考 https://www.jianshu.com/p/6e18d21a4cad
-
所给出的EDA步骤为广为普遍的步骤,在实际的不管是工程还是比赛过程中,这只是最开始的一步,也是最基本的一步。
接下来一般要结合模型的效果以及特征工程等来分析数据的实际建模情况,根据自己的一些理解,查阅文献,对实际问题做出判断和深入的理解。
最后不断进行EDA与数据处理和挖掘,来到达更好的数据结构和分布以及较为强势相关的特征
数据探索在机器学习中我们一般称为EDA(Exploratory Data Analysis):
是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索,通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。
数据探索有利于我们发现数据的一些特性,数据之间的关联性,对于后续的特征构建是很有帮助的。
- 对于数据的初步分析(直接查看数据,或.sum(), .mean(),.descirbe()等统计函数)可以从:样本数量,训练集数量,是否有时间特征,是否是时序问题,特征所表示的含义(非匿名特征),特征类型(字符类似,int,float,time),特征的缺失情况(注意缺失的在数据中的表现形式,有些是空的有些是”NAN”符号等),特征的均值方差情况。
- 分析记录某些特征值缺失占比30%以上样本的缺失处理,有助于后续的模型验证和调节,分析特征应该是填充(填充方式是什么,均值填充,0填充,众数填充等),还是舍去,还是先做样本分类用不同的特征模型去预测。
- 对于异常值做专门的分析,分析特征异常的label是否为异常值(或者偏离均值较远或者事特殊符号),异常值是否应该剔除,还是用正常值填充,是记录异常,还是机器本身异常等。
- 对于Label做专门的分析,分析标签的分布情况等。
- 进步分析可以通过对特征作图,特征和label联合做图(统计图,离散图),直观了解特征的分布情况,通过这一步也可以发现数据之中的一些异常值等,通过箱型图分析一些特征值的偏离情况,对于特征和特征联合作图,对于特征和label联合作图,分析其中的一些关联性。