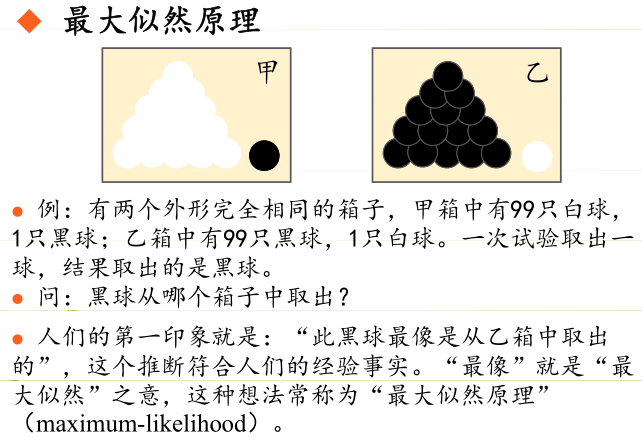
什么是极大似然估计
-
贝叶斯决策
首先来看贝叶斯分类,我们都知道经典的贝叶斯公式:$P(y | x)=\frac{p(x | y) p(y)}{p(x)}$,其中:$p(y)$ 为先验概率,表示每种类别分布的概率;$p(x | y)$ 为类条件概率,表示在某种类别前提下,某事发生的概率;$P(y | x)$ 为后验概率,表示某事发生了,并且它属于某一类别的概率。有了这个后验概率,我们就可以对样本进行分类。后验概率越大,说明某事物属于这个类别的可能性越大,我们越有理由把它归到这个类别下。
我们来看一个直观的例子:已知:在夏季,某公园男性穿凉鞋的概率为1/2,女性穿凉鞋的概率为2/3,并且该公园中男女比例通常为2:1,问题:若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
从问题看,就是上面讲的,某事发生了,它属于某一类别的概率是多少?即后验概率。
\[\text{设:}w_1 = \text{男性},w_2 = \text{女性},x = \text{穿凉鞋,由已知可得:}\] \[\text{先验概率:} p(w_1) = 2/3, p(w_2) = 1/3\] \[\text{类条件概率:} p(x \mid w_1) = 1/2, p(x \mid w_2) = 2/3\] \[\text{男性和女性穿凉鞋相互独立:} p(x)=p\left(x | w_{1}\right) p\left(w_{1}\right)+p\left(x | w_{2}\right) p\left(w_{2}\right)=5 / 9\]由贝叶斯公式算出:
\[\begin{array}{l}{P\left(w_{1} | x\right)=\frac{p\left(x | w_{1}\right) p\left(w_{1}\right)}{p(x)}=\frac{1 / 2 \times 2 / 3}{5 / 9}=\frac{3}{5}} \\ {P\left(w_{2} | x\right)=\frac{p\left(x | w_{2}\right) p\left(w_{2}\right)}{p(x)}=\frac{2 / 3 \times 1 / 3}{5 / 9}=\frac{2}{5}}\end{array}\] -
问题引出
- 但是在实际问题中并不都是这样幸运的,我们能获得的数据可能只有有限数目的样本数据,而先验概率 $p(w_i)$ 和类条件概率(各类的总体分布) $p(x \mid w_i)$ 都是未知的。根据仅有的样本数据进行分类时,一种可行的办法是我们需要先对先验概率和类条件概率进行估计,然后再套用贝叶斯分类器。
- 先验概率的估计较简单,1、每个样本所属的自然状态都是已知的(有监督学习);2、依靠经验;3、用训练样本中各类出现的频率估计。
-
类条件概率的估计(非常难),原因包括:概率密度函数包含了一个随机变量的全部信息;样本数据可能不多;特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是,把估计完全未知的概率密度 $p(x \mid w_i)$ 转化为估计参数。这里就将概率密度估计问题转化为参数估计问题,极大似然估计就是一种参数估计方法。当然了,概率密度函数的选取很重要,模型正确,在样本区域无穷时,我们会得到较准确的估计值,如果模型都错了,那估计半天的参数,肯定也没啥意义了。
-
重要前提
上面说到,参数估计问题只是实际问题求解过程中的一种简化方法(由于直接估计类条件概率密度函数很困难)。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。
- 重要前提:训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量($iid$ 条件),且有充分的训练样本。
-
极大似然估计
总结起来,最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
- 原理
- 极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
- 由于样本集中的样本都是独立同分布,可以只考虑一类样本集 $D$,来估计参数向量 $\theta$。记已知的样本集为:$D=\lbrace x_{1}, x_{2}, \cdots, x_{N} \rbrace$
-
似然函数: 联合概率密度函数 $P(D \mid \theta)$ 称为相对于 $\lbrace x_{1}, x_{2}, \cdots, x_{N} \rbrace$ 的 $\theta$ 的似然函数。
\[l(\theta)=p(D | \theta)=p\left(x_{1}, x_{2}, \cdots, x_{N} | \theta\right)=\prod_{i=1}^{N} p\left(x_{i} | \theta\right)\] -
如果 $\hat{\theta}$ 是参数空间中能使似然函数 $l(\theta)$ 最大的 $\theta$ 值,则 $\hat{\theta}$ 应该是“最可能”的参数值,那么 $\hat{\theta}$ 就是 $\theta$ 的极大似然估计量。它是样本集的函数,记作:
\[\hat{\theta} = d(x_{1}, x_{2}, \cdots, x_{N})=d(D)\\ \hat{\theta}(x_{1}, x_{2}, \cdots, x_{N})\text{称为极大似然函数的估计值}\]
- 原理
-
求解极大似然函数
-
ML估计:求使得出现该组样本的概率最大的 $\theta$ 值。
\[\hat{\theta}=\arg \max_{\theta} l(\theta)=\arg \max_{\theta} \prod_{i=1}^{N} p\left(x_{i} | \theta\right)\]
实际中为了便于分析,定义了对数似然函数:
\[\begin{array}{c}{H(\theta)=\ln l(\theta)} \\ {\hat{\theta}=\arg \max_{\theta} H(\theta)=\arg \max_{\theta} \ln l(\theta)=\arg \max_{\theta} \sum_{i=1}^{N} \ln p\left(x_{i} | \theta\right)}\end{array}\]- $1.$ 未知参数只有一个( $\theta$ 为标量)
在似然函数满足连续、可微的正则条件下,极大似然估计量是下面微分方程的解:
\[\frac{d l(\theta)}{d \theta}=0 \text{或者等价于} \frac{d H(\theta)}{d \theta}=\frac{d \ln l(\theta)}{d \theta}=0\] -
$2.$ 未知参数有多个( $\theta$ 为向量)
\[\nabla_{\theta} H(\theta)=\nabla_{\theta} \ln l(\theta)=\sum_{i=1}^{N} \nabla_{\theta} \ln P\left(x_{i} | \theta\right)=0\]
则 $\theta$ 可表示为具有 $S$ 个分量的未知向量:$\theta=\left[\theta_{1}, \theta_{2}, \cdots, \theta_{S}\right]^{T}$
记梯度算子:$\nabla_{\theta}=\left[\frac{\partial}{\partial \theta_{1}}, \frac{\partial}{\partial \theta_{2}}, \cdots, \frac{\partial}{\partial \theta_{S}}\right]^{T}$
若似然函数满足连续可导的条件,则最大似然估计量就是如下方程的解。
-
基础概念
-
先验概率、条件概率、后验概率
- 条件概率: 就是事件A(瓜的颜色是青绿)在事件B(瓜是好瓜)发生的条件下发生的概率。
- 条件概率 $p(x=\text{颜色是青绿} \mid y=\text{好瓜})$ ,就是在条件为瓜是好瓜的情况下,瓜的颜色是青绿的概率
- 先验概率: 在贝叶斯统计中,某一不确定量 p 的先验概率分布是在考虑”观测数据”前,能表达 p 不确定性的概率分布。它旨在描述这个不确定量的不确定程度,而不是这个不确定量的随机性。这个不确定量可以是一个参数,或者是一个隐含变量。
- 先验概率 $p(x=\text{颜色是青绿})$,就是常识、经验、统计学所透露出的“因”的概率,即瓜的颜色是青绿的概率。
- 后验概率: 在贝叶斯统计中,一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。同样,后验概率分布是一个未知量(视为随机变量)基于试验和调查后得到的概率分布。“后验”在本文中代表考虑了被测试事件的相关证据。
- 后验概率 $p(y=\text{好瓜} \mid x=\text{颜色是青绿})$,就是在知道“果”之后,去推测“因”的概率,也就是说,如果已经知道瓜是好瓜,那么瓜的颜色是青绿的概率是多少。后验和先验的关系就需要运用贝叶斯决策理论来求解。
- 条件概率: 就是事件A(瓜的颜色是青绿)在事件B(瓜是好瓜)发生的条件下发生的概率。
-
联合概率分布
-
Probability of two (or more) simultaneous events
-
朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布 $P(X,Y)$,然后求得后验概率分布 $P(Y \mid X)$ 。具体来说,利用训练数据学习 $P(X \mid Y)$ 和 $P(Y)$ 的估计,得到联合概率分布:
\[P(X,Y)=P(Y)P(X \mid Y)\]
-
-
条件概率分布
-
Probability of one (or more) event given the occurrence of another event
\[P\left(X=x | Y=c_{k}\right)=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} | Y=c_{k}\right), \quad k=1,2, \cdots, K\] -
条件概率分布 $P(X=x \mid Y=c_k)$ 有指数级的数量的参数,假设 $x^{(j)}$ 可取值有 $S_j$ 个,$j=1,2,…,n$,Y可取值有 K 个,那么参数个数为 $K\prod_{j=1}^{n}S_j$。因为 X 作为特征向量维度往往很大,任意特征组合在一起的概率都考虑的话几乎没法统计出来。
-
-
条件独立性假设
-
假设条件相互独立,求解的参数大大减少,只需要单独求解每一个 $p(x^i \mid y)$ 然后相乘。
\[\begin{aligned} P\left(X=x | Y=c_{k}\right) &=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} | Y=c_{k}\right) \\ &=\prod_{j=1}^{n} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right) \end{aligned}\] -
朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测,对给定的输入 x,通过学习到的模型计算后验概率分布$P(Y=c_k \mid X=x)$,将后验概率最大的类作为 x 的类输出。后验概率计算根据贝叶斯定理进行:
\[P\left(Y=c_{k} | X=x\right)=\frac{P(X,Y)}{P(X)}=\frac{P\left(X=x | Y=c_{k}\right) P\left(Y=c_{k}\right)}{\sum_{k} P\left(X=x | Y=c_{k}\right) P\left(Y=c_{k}\right)}\] \[\begin{array}{c} \\ {P\left(Y=c_{k} | X=x\right)=\frac{P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)},}\end{array}, \quad k=1,2, \cdots, K\]故朴素贝叶斯分类器可表示为:
\[y=f(x)=\arg \max_{c_{k}} \frac{P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}\] \[y=\arg \max_{c_{k}} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)\]
-
MLE vs. MAP

- MLE

-
MAP




特殊问题
-
下溢问题如何解决?
数值下溢问题:是指计算机浮点数计算的结果小于可以表示的最小数,因为计算机的能力有限,当数值小于一定数时,其无法精确保存,会造成数值的精度丢失,由上述公式可以看到,求概率时多个概率值相乘,得到的结果往往非常小;因此通常采用取对数的方式,将连乘转化为连加,以避免数值下溢。 -
零概率问题如何解决?
零概率问题,就是在计算实例的概率时,如果某个量x,在观察样本库(训练集)中没有出现过,会导致整个实例的概率结果是0.
朴素贝叶斯算法的先天缺陷:其他属性携带的信息被训练集中某个分类下未出现的属性值“抹去”,造成预测出来的概率绝对为0。为了拟补这一缺陷,前辈们引入了拉普拉斯平滑的方法:对先验概率的分子(划分的计数)加1,分母加上类别数;对条件概率分子加1,分母加上对应特征的可能取值数量。这样在解决零概率问题的同时,也保证了概率和依然为1:
python实现(代码链接)
实现naive bayes