What is Decision Tree
- Decision trees, as the name implies, are trees of decisions.
- A decision tree is a tree where each node represents a feature(attribute), each link(branch) represents a decision(rule) and each leaf represents an outcome(categorical or continues value).

Decision Tree algorithms







- 特征选择


-
划分选择
- 信息熵 Ent(D)
In the most layman terms, Entropy is nothing but the measure of disorder(Purity).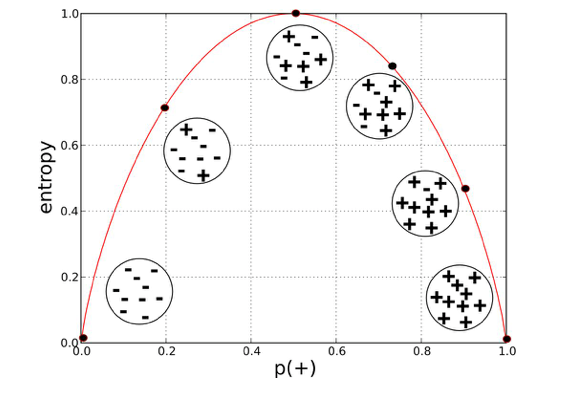
设随机标量X是一个离散随机变量,其概率分布为:$P(X=x_i)=p_i, i=1,2,…,n$,则随机变量X的熵定义为:$Ent(D)=-\sum_{i=1}^{n}p_ilog{p_i}$。Ent(D)值越小,则D的纯度越高。
- 信息增益 Gain(D,a)

一般来说,信息增益越大说明使用属性 a 进行划分所获得的“纯度提升”越大,因此我们可以用信息增益作为一种属性划分的选择。(选择属性 a 进行划分后,将不再作为候选的划分属性,即每个属性参与划分后就将其从候选集中移除)。
- 增益率 Gain_ratio(D,a)

-
基尼指数 Gini_index(D,a)

直观上的理解为,Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此,Gini(D)越小,则数据集D纯度越高。
- 信息熵 Ent(D)
-
剪枝处理
剪枝(pruning)是解决决策树过拟合的主要手段,通过剪枝可以大大提升决策树的泛化能力。通常,剪枝处理可分为:预剪枝,后剪枝。-
预剪枝:通过启发式方法,在生成决策树过程中对划分进行预测,若当前结点的划分不能对决策树泛化性能提升,则停止划分,并将其标记为叶节点。
-
后剪枝:对已有的决策树,自底向上的对非叶结点进行考察,若该结点对应的子树替换为叶结点能提升决策树的泛化能力,则将改子树替换为叶结点。
对于后剪枝策略,可以通过极小化决策树整体的损失函数(Cost function)来实现。设树T的叶节点个数为|T|,t是树T的叶结点,该叶节点有 $N_t$ 个样本点,其中k类的样本点有 $N_{tk}$ 个,k=1,2,…,K,$H_t(T)$为叶结点 t 上的经验熵,α≥0 为参数,则决策树学习的损失函数可以定义为:$$ C_{\alpha}(T)=\sum_{t=1}^{|T|} N_{t} H_{t}(T)+\alpha|T| $$
其中经验熵 $H_t(T)$ 为:$H_{t}(\mathrm{T})=-\sum_{\mathrm{k}} \frac{N_{t k}}{N_{t}} \log \frac{N_{t k}}{N_{t}}$
令C(T)表示模型对训练数据预测误差,即模型与训练数据的拟合程度,|T|表示模型的复杂度,参数α≥0调节二者关系。$$ \mathrm{C}(\mathrm{T})=\sum_{t=1}^{|T|} N_{t} H_{t}(T)=-\sum_{t=1}^{|T|} \sum_{k=1}^{K} N_{t k} \log \frac{N_{t k}}{N_{t}} $$
这时损失函数变为:$C_{\alpha}(T)=C(\mathrm{T})+\alpha \mid T \mid$。
$$ 模型损失=经验风险最小化+正则项=结构风险最小化 $$
较大的α促使树的结构更简单,较小的α促使树的结构更复杂,α=0意味着不考虑树的复杂度(α|T|就是正则项,加入约束,使得模型简单,避免过拟合)。
-
Input: 生成算法产生的整个决策树T,参数α
Output: 剪枝后的子树T’
Process:
1: 计算每个结点的经验熵
2: 递归地从树的叶结点向上回缩(参考下图)
设一组叶结点回缩到父结点之前与之后的整体树分别为T1于T2,
其对应的损失函数值分别为Cα(T1)和Cα(T2),
if Cα(T1)≤Cα(T2) then
进行剪枝(pruning)
end if
3: 返回第2步,直至不能继续为止,得到损失函数最小的子树T’
Regerssion Tree& Classification Tree


- Classification trees are designed for dependent variables that take a finite number
of unordered values, with prediction error measured in terms of misclassification cost. Regression trees are for dependent variables that take continuous or ordered discrete values, with prediction error typically measured by the squared difference between the observed and predicted values.
- The first published classification tree algorithm is THAID
- C4.5 and CART are two later classification tree algorithms
- Historically, the first regression tree algorithm is AID
- M5, an adaptation of a regression tree algorithm by Quinlan
sklearn.tree.DecisionTreeClassifier部分参数解析
| Parameters | detail |
|---|---|
| criterion:{“gini”, “entropy”}, default=”gini” | The function to measure the quality of a split. |
| splitter:{“best”, “random”}, default=”best” | The strategy used to choose the split at each node |
| max_depth:int, default=None | The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples. |
| min_samples_split:int or float, default=2 | The minimum number o r fractions of samples required to split an internal node |
| min_samples_leaf:int or float, default=1 | The minimum number of samples required to be at a leaf node |
| min_weight_fraction_leaf:float, default=0.0 | The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node |
| max_features:int, float or {“auto”, “sqrt”, “log2”}, default=None | The number of features to consider when looking for the best split |
python实现(代码链接)
实现自定义CART树