机器学习介绍
-
机器学习介绍:机器学习是什么,怎么来的,理论基础是什么,为了解决什么问题。
-
机器学习是什么?
-
什么是“学习”?学习就是人类通过观察、积累经验,掌握某项技能或能力。就好像我们从小学 习识别字母、认识汉字,就是学习的过程。而机器学习(Machine Learning),顾名思义, 就是让机器(计算机)也能向人类一样,通过观察大量的数据和训练,发现事物规律,获得某种分析问题、解决问题的能力。
-
Improving some performance measure with experence computed from data.
也就是机器从数据中总结经验,从数据中找出某种规律或者模型,并用它来解决实际问题。

-
-
为了解决什么问题
- 其应用场合大致可归纳为三个条件
- 事物本身存在某种潜在规律
- 某些问题难以使用普通编程解决
- 有大量的数据样本可供使用

- 其应用场合大致可归纳为三个条件
机器学习分类
-
Learning with Different Output Space Y
- 1.分类问题,输出都是离散值
- 二元分类(binary classification):输出只有两个,一般y={-1, +1}
- 包括信用卡发放、垃圾邮件判别、患者疾病诊断、答案正确性估计等
- 多元分类(Multiclass Classification):输出 多于两个,y={1, 2, … , K}, K>2
- 有数字识别、图片内容识别等
- 二元分类(binary classification):输出只有两个,一般y={-1, +1}
- 2.回归问题,输出y=R,即范围在整个实数空间, 是连续的
- 线性回归
- 预测房屋价格、股票收益多少等
- 线性回归
- 1.分类问题,输出都是离散值
-
Learning with Different Data Label yn
-
有监督:训练样本D既有输入特征x,也有输出yn
-
二元分类、多元分类或者是回归
-
判别模型与生成模型
-
-
半监督:一部分数据有输出标签yn,而另一部分数据没有输出标签yn
-
无监督:训练样本没有输出标签yn的
- 聚类、异常检测
-
强化学习:强化学习中,我们给模型或系统一些输 入,但是给不了我们希望的真实的输出y,根据模型的输出反馈,如果反馈结果良好,更接近真实输出,就给其正向激励,如果反馈结果不好,偏离真实输出,就给其反向激励。不断通过“反馈-修正”这种形式,一步一步让模型学习的更好,这就是强化学习的核心所在。
- 根据用户点击、选择而不断改进的广告系统
-
-
按任务类型分
-
回归
-
分类
-
聚类
-
生成模型与判别模型
-
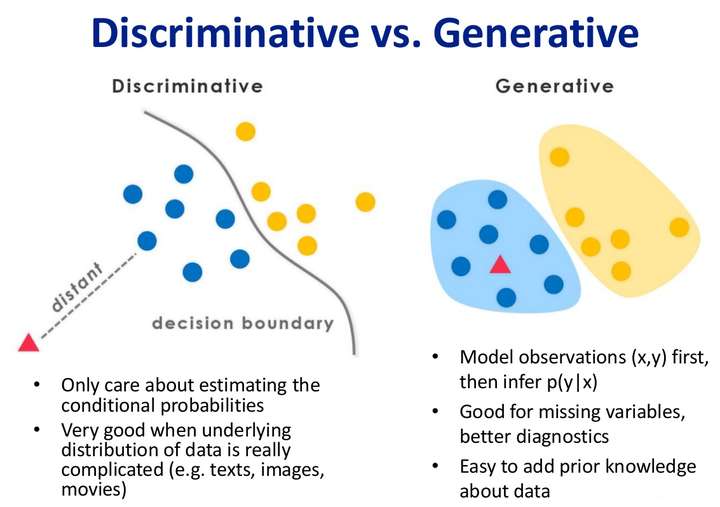
判别模型的重点在于用差别去分类;
-
生成模型是通过尝试知道(或者关注)数据是如何生成(就是去找到一个能够生成这些数据的分布,体现在数学上就是,找到的这个分布是一个联合分布),之后再对数据分类(体现在数学上就是用联合分算出属于某类别的条件概率,选条件概率最大的那个类别就是判断数据所属的类别)
-
二者目的都是在使后验概率最大化,判别式是直接对后验概率建模,但是生成模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率
- 判别式模型举例:要确定一个羊是山羊还是绵羊,用判别模型的方法是从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是山羊的概率,是绵羊的概率。
- 生成式模型举例:利用生成模型是根据山羊的特征首先学习出一个山羊的模型,然后根据绵羊的特征学习出一个绵羊的模型,然后从这只羊中提取特征,放到山羊模型中看概率是多少,在放到绵羊模型中看概率是多少,哪个大就是哪个。
- 生成模型:在概率统计理论中, 生成模型是指能够随机生成观测数据的模型,尤其是在给定某些隐含参数的条件下。它给观测值和标注数据序列指定一个联合概率分布。在机器学习中,生成模型可以用来直接对数据建模(例如根据某个变量的概率密度函数进行数据采样),也可以用来建立变量间的条件概率分布。条件概率分布可以由生成模型根据贝叶斯定理形成。常见的基于生成模型算法有高斯混合模型和其他混合模型、隐马尔可夫模型、随机上下文无关文法、朴素贝叶斯分类器、AODE分类器、潜在狄利克雷分配模型、受限玻尔兹曼机
- 举例:要确定一个瓜是好瓜还是坏瓜,用判别模型的方法是从历史数据中学习到模型,然后通过提取这个瓜的特征来预测出这只瓜是好瓜的概率,是坏瓜的概率。
- 判别模型: 在机器学习领域判别模型是一种对未知数据 y 与已知数据 x 之间关系进行建模的方法。判别模型是一种基于概率理论的方法。已知输入变量 x ,判别模型通过构建条件概率分布 $P(y \mid x)$ 预测 y 。常见的基于判别模型算法有逻辑回归、线性回归、支持向量机、提升方法、条件随机场、人工神经网络、随机森林、感知器
- 举例:利用生成模型是根据好瓜的特征首先学习出一个好瓜的模型,然后根据坏瓜的特征学习得到一个坏瓜的模型,然后从需要预测的瓜中提取特征,放到生成好的好瓜的模型中看概率是多少,在放到生产的坏瓜模型中看概率是多少,哪个概率大就预测其为哪个。
- 生成模型是所有变量的全概率模型,而判别模型是在给定观测变量值前提下目标变量条件概率模型。因此生成模型能够用于模拟(即生成)模型中任意变量的分布情况,而判别模型只能根据观测变量得到目标变量的采样。判别模型不对观测变量的分布建模,因此它不能够表达观测变量与目标变量之间更复杂的关系。因此,生成模型更适用于无监督的任务,如分类和聚类。
-
-
机器学习方法三要素
-
模型
- 就是要学习的概率分布或决策函数 所有可能的条件概率分布或者决策函数构成的集合就是模型的假设空间
- 策略
- 从假设空间中学习最优模型的方法,称为策略
衡量模型好与不好需要一些指标,这时引入风险函数和损失函数来衡量。预测值和真实值通常是不想等的,我们用损失函数或代价函数来度量预测错误的程度,记作 L(Y,f(x))
- 0~1损失函数
$$ L(y,f(x)) = \begin{cases} 0, & \text{y = f(x)} \\ 1, & \text{y $\neq$ f(x)} \end{cases} $$
- 平方损失函数
$$ L(y,f(x))=|y-f(x)| $$
- 绝对损失函数
$$ L(y,f(x))=(y-f(x))^2 $$
- 对数损失函数
$$ L(y,f(x))=log(1+e^{-yf(x)}) $$
- 指数损失函数
$$ L(y,f(x))=exp(-yf(x)) $$
- Hinge损失函数
$$ L(w,b)=max\{0,1-yf(x)\} $$
- 0~1损失函数
- 从假设空间中学习最优模型的方法,称为策略
衡量模型好与不好需要一些指标,这时引入风险函数和损失函数来衡量。预测值和真实值通常是不想等的,我们用损失函数或代价函数来度量预测错误的程度,记作 L(Y,f(x))
-
算法
- 是指学习模型时的具体计算方法,求解最优模型归结为一个最优化问题,统计学习的算法等价于求解最优化问题的算法,也就是求解析解或数值解
- 批量梯度下降(BGD)
$$ \theta=\theta-\eta\nabla_\theta J(\theta) $$
- 随机梯度下降法(SGD)
$$ \theta=\theta-\eta\nabla_\theta J(\theta;x^{(i)},y^{(i)}) $$
- 小批量梯度下降
$$ \theta=\theta-\eta\nabla_\theta J(\theta;x^{(i:i+n)},y^{(i:i+n)}) $$
- 引入动量的梯度下降
$$ \begin{cases} v_t=\gamma v_{t-1}+\eta \nabla_\theta J(\theta) \\ \theta=\theta-v_t \end{cases} $$
- 自适应学习率的Adagrad算法
$$ \begin{cases} g_t= \nabla_\theta J(\theta) \\ \theta_{t+1}=\theta_{t,i}-\frac{\eta} {\sqrt{G_t+\varepsilon}} \cdot g_t \end{cases} $$
- 批量梯度下降(BGD)
- 模型评估指标
- MSE(Mean Squared Error)
$$ MSE(y,f(x))=\frac{1}{N}\sum_{i=1}^{N}(y-f(x))^2 $$
- MAE(Mean Absolute Error)
$$ MAE(y,f(x))=\frac{1}{N}\sum_{i=1}^{N}|y-f(x)| $$
- RMSE(Root Mean Squard Error)
$$ RMSE(y,f(x))=\frac{1}{1+MSE(y,f(x))} $$
- R方 R square
- 以上评价指标都无法消除量纲不一致而导致的误差值差别大的问题,最常用的指标是$R^2$,可以避免量纲不一致问题
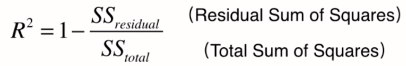
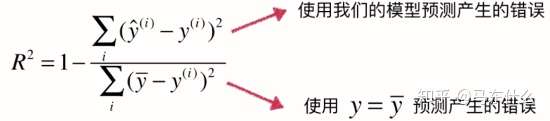
- 上:y预测 - y真,our model
- 下:y真平均 - y真,baseline model
- 我们可以把 $R^2$ 理解为,回归模型可以成功解释的数据方差部分在数据固有方差中所占的比例, $R^2$ 越接近1,表示可解释力度越大,模型拟合的效果越好。
- Confusion Matrix

- 真正例(True Positive, TP):You predicted positive and it’s true
- 假负例(False Negative, FN): You predicted negative and it’s false
- 假正例(False Positive, FP): You predicted positive and it’s false
- 真负例(True Negative, TN): You predicted negative and it’s true
- 准确率(Accuracy)
$$ ACC=\frac{TP+TN}{TP+FN+FP+TN} $$
- 精准率(Precision)
- Out of all the positive classes we have predicted, how many are actually positive
$$ P=\frac{TP}{TP+FP} $$
- 召回率(Recall/TPR/Sensitivity)
- Out of all the positive classes, how much we predicted correctly. It should be high as possible.
$$ R=\frac{TP}{TP+FN} $$
- F1-Score
- F-score helps to measure Recall and Precision at the same time. It uses Harmonic Mean in place of Arithmetic Mean by punishing the extreme values more.
$$ \frac{2}{F_1}=\frac{1}{P}+\frac{1}{R} $$
- Specificity
$$ Specificity=\frac{TN}{TN+FP} $$
- FPR = 1-Specificity
$$ FPR=\frac{FP}{TN+FP} $$
-
AUC - ROC Curve
- AUC - ROC curve is a performance measurement for classification problem at various thresholds settings. ROC is a probability curve and AUC represents degree or measure of separability. It tells how much model is capable of distinguishing between classes.

AUC ROC 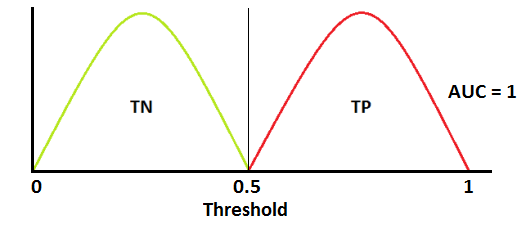







- MSE(Mean Squared Error)
- 复杂度度量
- 偏差与方差
- What is bias?
- Bias is the difference between the average prediction of our model and the correct value which we are trying to predict
- What is variance?
- Variance is the variability of model prediction for a given data point or a value which tells us spread of our data



- What is bias?
- 偏差与方差
- 可避免偏差&可避免方差


- Avoidable Bias = Difference (Training Error, Human-Level Performance)
- Variance = Difference (Development Error, Training Error)
-
Scenario A:
7% > 2% -》高偏差(可避免偏差大于方差) -
Scenario B:
0.5% < 2% -》高方差(可避免偏差小于方差)
-
- 过拟合与欠拟合

-
欠拟合
一般表示模型对数据的表现能力不足,通常是模型的复杂度不够,并且Bias高,训练集的损失值高,测试集的损失值也高. -
过拟合
一般表示模型对数据的表现能力过好,通常是模型的复杂度过高,并且Variance高,训练集的损失值低,测试集的损失值高. - 结构风险与经验风险
- 经验风险:是对训练集中的所有样本点损失函数的平均最小化
- 经验风险越小说明模型f(X)对训练集的拟合程度越好
- 期望风险:
- 未知的样本数据(<X,Y>)的数量是不容易确定的,所以就没有办法用所有样本损失函数的平均值的最小化这个方法,那么怎么来衡量这个模型对所有的样本(包含未知的样本和已知的训练样本)预测能力呢?熟悉概率论的很容易就想到了用期望。
- 经验风险是局部的,基于训练集所有样本点损失函数最小化的。
- 期望风险是全局的,是基于所有样本点的损失函数最小化的。
- 未知的样本数据(<X,Y>)的数量是不容易确定的,所以就没有办法用所有样本损失函数的平均值的最小化这个方法,那么怎么来衡量这个模型对所有的样本(包含未知的样本和已知的训练样本)预测能力呢?熟悉概率论的很容易就想到了用期望。
- 结构风险:
- 只考虑经验风险的话,会出现过拟合的现象,过拟合的极端情况便是模型f(x)对训练集中所有的样本点都有最好的预测能力,但是对于非训练集中的样本数据,模型的预测能力非常不好。怎么办呢?这个时候就引出了结构风险。结构风险是对经验风险和期望风险的折中。在经验风险函数后面加一个正则化项(惩罚项)便是结构风险了。
- 经验风险:是对训练集中的所有样本点损失函数的平均最小化
- 泛化能力
- 泛化能力通俗来讲就是指学习到的模型对未知数据的预测能力
- 提高泛化能力的方式大致有三种:1.增加数据量。2.正则化。3.凸优化。
- 正则化
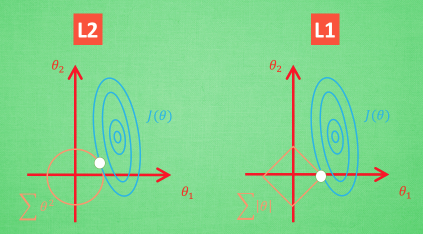
- Lasso(L1)
- for lasso, the equation becomes, |β1|+|β2|≤ s

- for lasso, the equation becomes, |β1|+|β2|≤ s
- Ridge Regression(L2)
- ridge regression is expressed by β1² + β2² ≤ s

- ridge regression is expressed by β1² + β2² ≤ s
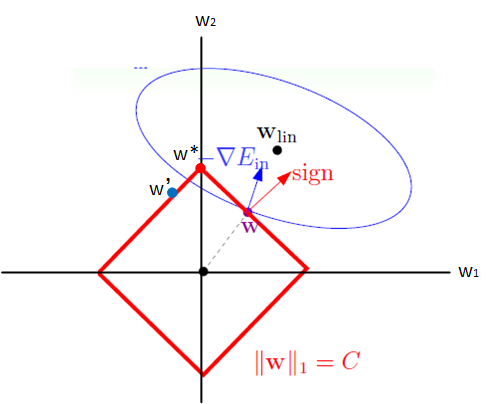
- 想象现在只有两个参数 theta1 theta2 要学, 蓝色的圆心是误差最小的地方, 而每条蓝线上的误差都是一样的. 正规化的方程是在黄线上产生的额外误差(也能理解为惩罚度), 在黄圈上的额外误差也是一样. 所以在蓝线和黄线交点上的点能让两个误差的合最小. 这就是 theta1 和 theta2 正规化后的解. 要提到另外一点是, 使用 L1 的方法, 我们很可能得到的结果是只有 theta1 的特征被保留, 所以很多人也用 L1 正规化来挑选对结果贡献最大的重要特征. 但是 L1 的结并不是稳定的. 比如用批数据训练, 每次批数据都会有稍稍不同的误差曲线。
-
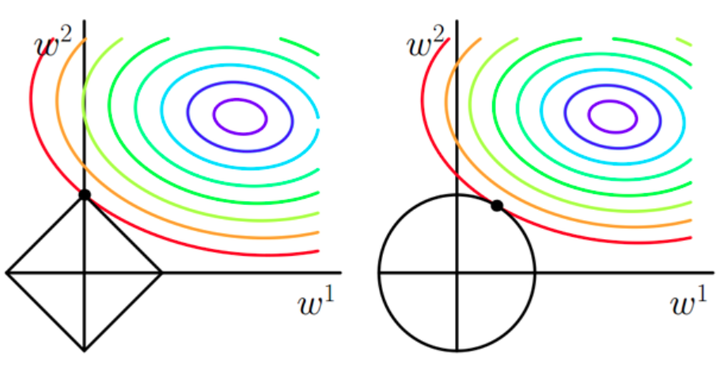
如果不加L1和L2正则化的时候,对于线性回归这种目标函数凸函数的话,我们最终的结果就是最里边的紫色的小圈圈等高线上的点。
- 当加入L1正则化的时候,我们现在的目标是不仅是原曲线算得值要小(越来越接近中心的紫色圈圈),还要使得这个菱形越小越好(F越小越好)。那么还和原来一样的话,过中心紫色圈圈的那个菱形明显很大,因此我们要取到一个恰好的值。那么如何求值呢?
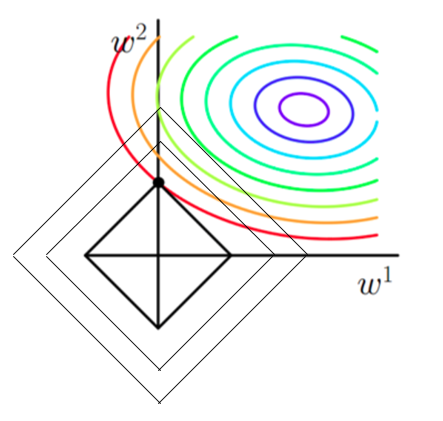
- L1正则为什么可以得到稀疏解?
L2 L1 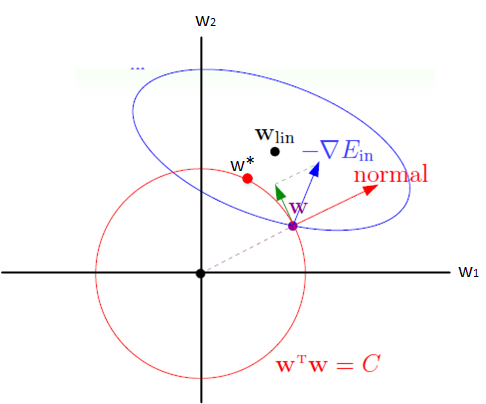
- Lasso(L1)
-
-
模型选择
- 正则化
- 交叉验证
- 交叉验证是在机器学习建立模型和验证模型参数时常用的办法,一般被用于评估一个机器学习模型的表现。更多的情况下,我们也用交叉验证来进行模型选择(model selection)。
- 交叉验证,顾名思义,就是重复地使用数据,把得到的样本数据进行切分,组合为不同的训练集和测试集,用训练集来训练模型,用测试集来评估模型预测的好坏。在此基础上可以得到多组不同的训练集和测试集,某次训练集中的某样本在下次可能成为测试集中的样本,即所谓“交叉”。
- 那么什么时候才需要交叉验证呢?交叉验证用在数据不是很充足的时候。如果数据样本量小于一万条,我们就会采用交叉验证来训练优化选择模型。如果样本大于一万条的话,我们一般随机的把数据分成三份,一份为训练集(Training Set),一份为验证集(Validation Set),最后一份为测试集(Test Set)。用训练集来训练模型,用验证集来评估模型预测的好坏和选择模型及其对应的参数。把最终得到的模型再用于测试集,最终决定使用哪个模型以及对应参数。
- 第一种是简单交叉验证,所谓的简单,是和其他交叉验证方法相对而言的。首先,我们随机的将样本数据分为两部分(比如: 70%的训练集,30%的测试集),然后用训练集来训练模型,在测试集上验证模型及参数。接着,我们再把样本打乱,重新选择训练集和测试集,继续训练数据和检验模型。最后我们选择损失函数评估最优的模型和参数。
- 第二种是 S折交叉验证( S-Folder Cross Validation),也是经常会用到的。和第一种方法不同, S折交叉验证先将数据集 D 随机划分为 S 个大小相同的互斥子集,每次随机的选择 S-1 份作为训练集,剩下的1份做测试集。当这一轮完成后,重新随机选择 S-1 份来训练数据。若干轮(小于 S )之后,选择损失函数评。
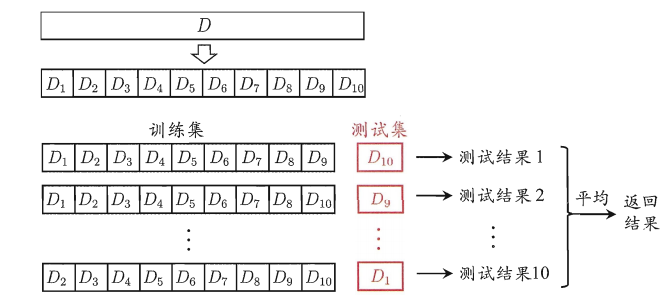
- 第三种是留一交叉验证(Leave-one-out Cross Validation),它是第二种情况的特例,此时 S等于样本数N ,这样对于 N 个样本,每次选择 N-1 个样本来训练数据,留一个样本来验证模型预测的好坏。此方法主要用于样本量非常少的情况,比如对于普通适中问题, N 小于50时,我一般采用留一交叉验证。
- 采样:样本不均衡
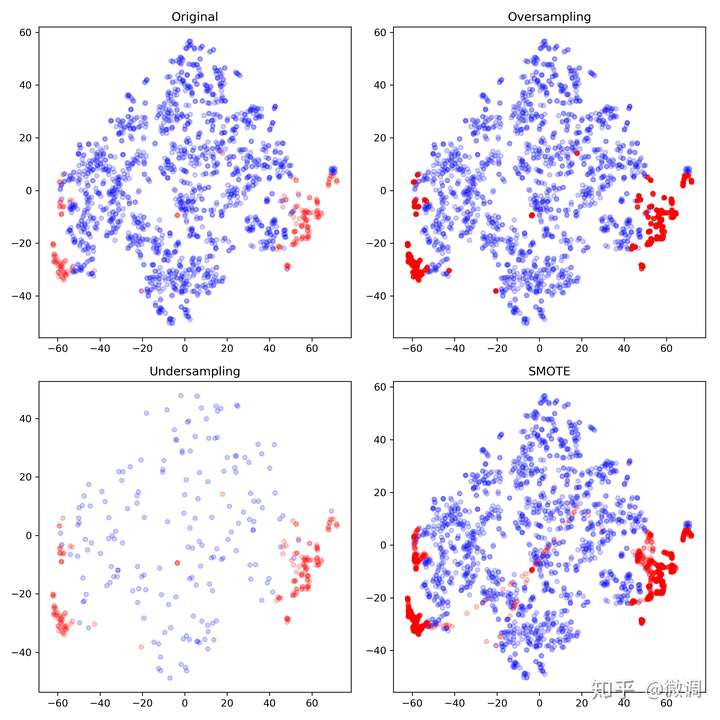
- 原始数据(Original):未经过任何采样处理
- 欠采样(Undersampling):从反例中随机选择176个数据,与正例合并
- 过采样(Oversampling):从正例中反复抽取并生成1655个数据(势必会重复),并与反例合并
- SMOTE:也是一种过采样方法。SMOTE通过找到正例中数据的近邻,来合成新的1655-176=1479个“新正例”,并与原始数据合并。此处应注意SMOTE并不是简单的重复,而是一种基于原始数据的生成。
1. 过采样(右上)只是单纯的重复了正例,因此会过分强调已有的正例。如果其中部分点标记错误或者是噪音,那么错误也容易被成倍的放大。因此最大的风险就是对正例过拟合。
2. 欠采样(左下)抛弃了大部分反例数据,从而弱化了中间部分反例的影响,可能会造成偏差很大的模型。当然,如果数据不平衡但两个类别基数都很大,或许影响不大。同时,数据总是宝贵的,抛弃数据是很奢侈的,因此另一种常见的做法是反复做欠采样,生成1655/176=9个新的子样本。其中每个样本的正例都使用这176个数据,而反例则从1655个数据中不重复采样。最终对这9个样本分别训练,并集成结果。这样数据达到了有效利用,但也存在风险:
- 训练多个模型造成了过大的开销,合并模型结果需要额外步骤,有可能造成其他错误
- 正例被反复使用,和过采样一样,很容易造成模型的过拟合
3. SMOTE(右下)可以看出和过采样(右上)有了明显的不同,因为不单纯是重复正例了,而是在局部区域通过K-近邻生成了新的正例。相较于简单的过采样, SMOTE:
- 降低了过拟合风险。K近邻在局部合成数据可以被理解为一种集成学习,降低了方差。但或许也错误的加强了局部的偶然性,从而增加了过拟合风险。但一般来看,优点大于风险
- 也可以理解为一种过采样的soft version,对于噪音的抵抗性更强
- 缺点也有,比如运算开销加大,同时可能会生成一些“可疑的点”,如下图所示
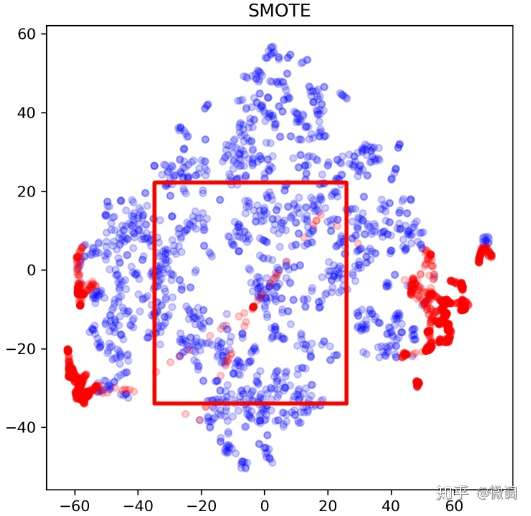
- 是指学习模型时的具体计算方法,求解最优模型归结为一个最优化问题,统计学习的算法等价于求解最优化问题的算法,也就是求解析解或数值解
-
特征处理
- 归一化、标准化、离散化、one-hot编码
-
模型调优
-
网格搜索
-
网格搜索是应用最广泛的超参数搜索算法,网格搜索通过查找搜索范围内的所有的点,来确定最优值。一般通过给出较大的搜索范围以及较小的步长,网格搜索是一定可以找到全局最大值或最小值的。但是,网格搜索一个比较大的问题是,它十分消耗计算资源,特别是需要调优的超参数比较多的时候。在比赛中,需要调参的模型数量与对应的超参数比较多,而涉及的数据量又比较大,因此相当的耗费时间。此外,由于给出的超参数组合比较多,因此一般都会固定多数参数,分步对1~2个超参数进行调解,这样能够减少时间但是缺难以自动化进行,而且由于目标参数一般是非凸的,因此容易陷入局部最小值。
import lightgbm as lgb from sklearn.model_selection import GridSearchCV def GridSearch(clf, params, X, y): cscv = GridSearchCV(clf, params, scoring='neg_mean_squared_error', n_jobs=1, cv=5) cscv.fit(X, y) print(cscv.cv_results_) print(cscv.best_params_) if __name__ == '__main__': train_X, train_y = get_data() param = { 'objective': 'regression', 'n_estimators': 275, 'max_depth': 6, 'min_child_samples': 20, 'reg_lambd': 0.1, 'reg_alpha': 0.1, 'metric': 'rmse', 'colsample_bytree': 1, 'subsample': 0.8, 'num_leaves' : 40, 'random_state': 2018 } regr = lgb.LGBMRegressor(**param) adj_params = {'n_estimators': range(100, 400, 10), 'min_child_weight': range(3, 20, 2), 'colsample_bytree': np.arange(0.4, 1.0), 'max_depth': range(5, 15, 2), 'subsample': np.arange(0.5, 1.0, 0.1), 'reg_lambda': np.arange(0.1, 1.0, 0.2), 'reg_alpha': np.arange(0.1, 1.0, 0.2), 'min_child_samples': range(10, 30)} GridSearch(regr , adj_params , train_X, train_y)
-
-
随机搜索
-
与网格搜索相比,随机搜索并未尝试所有参数值,而是从指定的分布中采样固定数量的参数设置。它的理论依据是,如果随机样本点集足够大,那么也可以找到全局的最大或最小值,或它们的近似值。通过对搜索范围的随机取样,随机搜索一般会比网格搜索要快一些。但是和网格搜索的快速版(非自动版)相似,结果也是没法保证的。
import lightgbm as lgb from sklearn.model_selection import RandomizedSearchCV def RandomSearch(clf, params, X, y): rscv = RandomizedSearchCV(clf, params, scoring='neg_mean_squared_error', n_jobs=1, cv=5) rscv.fit(X, y) print(rscv.cv_results_) print(rscv.best_params_) if __name__ == '__main__': train_X, train_y = get_data() param = { 'objective': 'regression', 'n_estimators': 275, 'max_depth': 6, 'min_child_samples': 20, 'reg_lambd': 0.1, 'reg_alpha': 0.1, 'metric': 'rmse', 'colsample_bytree': 1, 'subsample': 0.8, 'num_leaves' : 40, 'random_state': 2018 } regr = lgb.LGBMRegressor(**param) adj_params = {'n_estimators': range(100, 400, 10), 'min_child_weight': range(3, 20, 2), 'colsample_bytree': np.arange(0.4, 1.0), 'max_depth': range(5, 15, 2), 'subsample': np.arange(0.5, 1.0, 0.1), 'reg_lambda': np.arange(0.1, 1.0, 0.2), 'reg_alpha': np.arange(0.1, 1.0, 0.2), 'min_child_samples': range(10, 30)} RandomSearch(regr , adj_params , train_X, train_y)
-
-
贝叶斯优化
-
贝叶斯优化用于机器学习调参由J. Snoek(2012)提出,主要思想是,给定优化的目标函数(广义的函数,只需指定输入和输出即可,无需知道内部结构以及数学性质),通过不断地添加样本点来更新目标函数的后验分布(高斯过程,直到后验分布基本贴合于真实分布。简单的说,就是考虑了上一次参数的信息,从而更好的调整当前的参数。
-
贝叶斯优化与常规的网格搜索或者随机搜索的区别是:
1.贝叶斯调参采用高斯过程,考虑之前的参数信息,不断地更新先验;网格搜索未考虑之前的参数信息。 2.贝叶斯调参迭代次数少,速度快;网格搜索速度慢,参数多时易导致维度爆炸。 3.贝叶斯调参针对非凸问题依然稳健;网格搜索针对非凸问题易得到局部优最。
pip install bayesian-optimizationimport lightgbm as lgb from bayes_opt import BayesianOptimization train_X, train_y = None, None def BayesianSearch(clf, params): """贝叶斯优化器""" # 迭代次数 num_iter = 25 init_points = 5 # 创建一个贝叶斯优化对象,输入为自定义的模型评估函数与超参数的范围 bayes = BayesianOptimization(clf, params) # 开始优化 bayes.maximize(init_points=init_points, n_iter=num_iter) # 输出结果 params = bayes.res['max'] print(params['max_params']) return params def GBM_evaluate(min_child_samples, min_child_weight, colsample_bytree, max_depth, subsample, reg_alpha, reg_lambda): """自定义的模型评估函数""" # 模型固定的超参数 param = { 'objective': 'regression', 'n_estimators': 275, 'metric': 'rmse', 'random_state': 2018} # 贝叶斯优化器生成的超参数 param['min_child_weight'] = int(min_child_weight) param['colsample_bytree'] = float(colsample_bytree), param['max_depth'] = int(max_depth), param['subsample'] = float(subsample), param['reg_lambda'] = float(reg_lambda), param['reg_alpha'] = float(reg_alpha), param['min_child_samples'] = int(min_child_samples) # 5-flod 交叉检验,注意BayesianOptimization会向最大评估值的方向优化,因此对于回归任务需要取负数。 # 这里的评估函数为neg_mean_squared_error,即负的MSE。 val = cross_val_score(lgb.LGBMRegressor(**param), train_X, train_y ,scoring='neg_mean_squared_error', cv=5).mean() return val if __name__ == '__main__': # 获取数据,这里使用的是Kaggle比赛的数据 train_X, train_y = get_data() # 调参范围 adj_params = {'min_child_weight': (3, 20), 'colsample_bytree': (0.4, 1), 'max_depth': (5, 15), 'subsample': (0.5, 1), 'reg_lambda': (0.1, 1), 'reg_alpha': (0.1, 1), 'min_child_samples': (10, 30)} # 调用贝叶斯优化 BayesianSearch(GBM_evaluate, adj_params)
-
-
[machine learning algorithm cheat sheet]

